
(강의 내용 정리에 사용되는 자료의 출처는 저자님의 강의입니다. 출처 - 코딩 테스트 합격자 되기 [박경록])
(자료를 참고해서 제가 시각적으로 더 보기 편하게 편집한 사진들도 있습니다.)
한참 전에 작성했어야 했는데 대학원 입학서류 작성 + ADsP 자격증 시험공부로 인해 엄청나게 미뤄지게 되었습니다
거의 5월부터 입학을 희망해서 준비했는데 서류 광탈로 끝나서 허무함으로 잠시 공부를 손에 놓았습니다
그렇지만 입학 or 취업을 성공하려면 다시 공부해야죠 ㅠㅠ... 부족한 스펙을 다시 쌓기 위해
▶ 강의 목차
- 트리 개념
- 이진트리 표현
- 이진트리 순회
- 이진탐색트리
▶ 강의 내용 정리
- 트리의 개념
- 노드와 간선으로 이루어진 계층적 자료구조 (부모-자식 관계 존재)
- 위아래가 있다고 보면 된다!
- 사장님, 부사장님, 개발팀장, 구매팀장, 영업팀장 등의 구조
- 순환을 허용하지 않음
- 코딩테스트에서는 이진트리(자식 노드가 최대 2개인 트리)만 알면 된다
- 노드와 간선으로 이루어진 계층적 자료구조 (부모-자식 관계 존재)

- 루트노드
- 나무의 뿌리 같은 느낌. 자료구조에서 최상위에 존재
- 트리에서 유일함, 트리의 루트 노드는 {1}이다!
- 그림 설명
- 노드 {5}의 왼쪽 자식 노드는 {51}
- 노드 {5}의 오른쪽 자식 노드는 {4}
- 노드 {5}의 자식노드는 {4,51}이므로 자식 노드가 2개
- 노드 {51,4}의 부모 노드는 {5} (당연)
- 노드 {7}과 {5}는 형제 노드(부모가 같음)
- 노드 {3}은 자식이 없으므로 리프 노드 (잎사귀 느낌)
- 루트노드의 차수는 3(자식의 개수를 차수라고 함)
- 노드 {3,7,5}의 레벨은 2(루트노드에서 간선 2개로 갈 수 있음)
- TMI. 레벨이라는 거는 부모로부터 몇 개의 간선을 거쳐 갈 수 있느냐는 의미
- 레벨 값 중 가장 큰 게 3이므로 높이는 3이다
- TMI. 루트노드로부터 가장 깊이 들어갈 수 있는 노드가 높이
- 이진 트리 표현 하기 (배열)
- 루트 노드 인덱스는 1
- 0으로 하면 안 되는 건가요? 배열의 인덱스를 아끼고 싶은데....
- 하지만 계산을 편하게 하기 위해서는 인덱스 0을 버리고 1부터 시작하는 게 편리함!!
- 왼쪽 자식 노드는 부모노드 인덱스 * 2
- 오른쪽 자식 노드는 부모노드 인덱스 * 2 + 1
- 인덱스 공식만 활용하므로 구현난이도가 낮음
- 근데 인덱스에 빈 공간이 많아서 메모리 효율은 떨어질 수 있음. 하지만 구현은 쉽다는 장점!
- 루트 노드 인덱스는 1

- 이진 트리 표현하기(인접 리스트)
- 각 리스트의 인덱스는 부모 노드
- 자식 노드는 부모 노드에 해당되는 인덱스에 추가
- 공간활용도가 높음. 노드 자체를 실제 트리의 노드 개수와 비슷하게 만들면 되기 때문
- 배열보다 공간 효율이 좋음
- 자식 노드를 찾는데 오래 걸릴 수 있음
- 순차탐색 필요함
- 이진트리는 자식이 2개이므로 크게 단점이 없음
- 대부분의 코테 문제는 이진 트리 문제이므로 인접 리스트가 비효율적인 경우는 없음!

- 이진 트리의 순회
- 트리의 노드를 모두 방문하는 방법
- 현재노드를 언제 방문하는지에 따라 전위순회, 중위순회, 후위순회로 분류됨
- 이진 트리의 순회(전위 순회)
- 부모 노드 → 왼쪽 자식 노드 → 오른쪽 자식 노드 순으로 방문함
- 루트노드부터 시작
- 아래에 그림과 설명이 있는데 절대 어렵지 않음! 천천히 읽으면 이해가능








- 이 과정을 한 STEP 설명 보니까 이해되네! 가 아니라 트리가 주어지면 설명한 대로 자연스럽게 되어야 함
- 또한 코드도 작성할 수 있어야 함!
- 이진 트리의 순회(전위 순회의 실 예시)
- 트리 복사
- 루트노드부터 트리 노드를 순차적으로 복사할 수 있음
- 1, 4, 3, 2, 5, 8, 7, 6 순서대로 복사함(부모부터 차례대로 복사되는 걸 알 수 있음)

- 이진 트리의 순회(중위 순회)
- 왼쪽 자식 노드 → 부모 노드 → 오른쪽 자식 노드 순으로 방문
- 루트 노드부터 시작












- 이진 트리의 순회(중위 순회의 실 예시)
- 이진탐색트리의 원소를 정렬된 상태로 순회(왼쪽은 부모보다 작다 / 오른쪽은 크다)
- 순회순서 : 1 → 2 → 3 → 4 → 5 → 6 → 7
- 왼 → 본 → 오

- 이진 트리의 순회(후위 순회)
- 왼쪽 자식 노드 → 오른쪽 자식 노드 → 부모 노드 순으로 방문함
- 루트노드부터 시작
- 아래부터 채워간다는 느낌적인 느낌












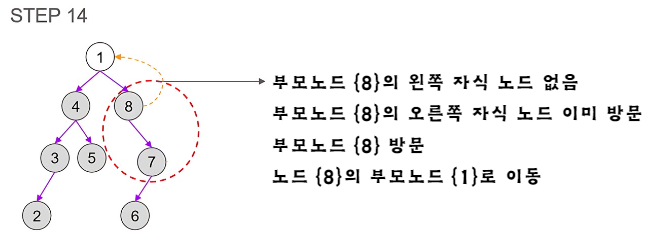

- 이진 트리의 순회(후위 순회의 실 예시)
- 폴더 삭제 하기
- → 제일 깊숙이 들어있는 폴더부터 삭제해야 함
- 트리를 삭제할 때 후위 순회 사용하면 된다~

- 이진 탐색 트리의 개념
- 탐색을 효율적으로 하기 위해 만든 이진 트리
- 왼쪽 자식 노드는 부모 노드보다 작은 값
- 오른쪽 자식 노드는 부모 노드보다 큰 값
- 이진 탐색 트리 삽입
- 중위 순회를 통해서 순서 확인 가능

- 이진 탐색 트리를 활용한 탐색의 효율
- 왜 이진 탐색 트리를 활용?
- 결론적으로 높이 h 만큼 탐색할 것임 (최악의 경우)
- 그냥 정렬하게 되면 효율이 떨어짐 N log N
- 이진탐색트리 활용하면 log N이므로 더 효율적

- 이진 탐색 트리 특성
- 최대 탐색 횟수는 트리의 높이와 같다. (최악의 경우 O(N)이지만 균형 유지 시 O(logN))
- 삽입과 동시에 정렬을 한다 (최악의 경우 O(N)이지만 균형 유지시 O(logN))
- map, set의 내부는 균형이진탐색트리로 되어있음(키값 기준 정렬 O)
- C++에서 많이 실수하는 부분 1
- *unordered_가 붙은 STL은 해시임(키값기준 정렬 X)
-
- C++에서 많이 실수하는 부분 2
-
순회는 코드를 꼭 작성해서 익혀야 함!
보기만 해서 이해하기 어려운 부분이기 때문

▶ 후기
-
- 몇주 전에 절반이상 작성해두었다가 개인적인 사정으로 미루다 이제서야 나머지를 수강해서 작성했습니다.
- 5월부터 입학을 준비한 대학원의 꿈이 공중분해 되어서 머리에 블루스크린이 떴는데, 미뤘던 부분들도 빠르게 수강해서 정리 글을 올려보겠습니다 ㅜ
- 코테 문제를 풀다가 추가로 알게된 부분은 추후 추가하겠습니다.
'그룹 스터디(책 기반으로) > 코딩테스트 합격자 되기 C++' 카테고리의 다른 글
| 코테 스터디 3주차 [해시] (2) | 2024.10.16 |
|---|---|
| 혼자 읽기 아쉬운 저자님의 당부사항 (1) | 2024.10.16 |
| 코테 스터디 2주차 [스택/큐] (3) | 2024.10.15 |


